利用 AOTF 近红外光谱仪检测中药中微生物的方法
摘 要 本文采用 AOTF 近红外光谱技术以漫反射方式对新癀片中的微生物即细菌和霉菌进 行光谱扫描,分别建立了偏最小二乘法(PLS1)回归模型和主成分分析模型。通过偏最小二 乘法(PLS1),建立了菌体数量的回归模型,并探讨了菌体数量梯度对模型预测结果的影响, 最终确定了以多模型分步快速菌检法的预测方法。通过主成分分析模型,结果显示 AOTF 技 术建立的数学模型不仅能够分辨出样品中的菌体数量是否合格,还能够对菌体是否具有活性 进行定性。实验结果表明,AOTF-NIR Luminar 5030 光谱仪利用使用光谱数据和校准模型, 能够快速准确地对新癀片中的菌体进行定量分析和定性分析。
主题词 声光可调滤光器;近红外光谱;微生物;偏最小二乘法(PLS1)
在中药制药行业,对细菌等微生物的的检测按照国家药典的规定是必须进行的一项检测 项目,常规的检测方法是利用培养基培养计数的方式来进行检测[1],该方法操作复杂、费时 费力,至少需要 48 小时才能得到最终的检测结果,不能够保持一个流畅的生产过程。如何 寻找一种快速的检测方式,能够迅速得到检验结果,对中药制药行业的生产具有重大的意义。 近几年在中国兴起的近红外检测技术,作为一门独立的分析检测技术具有不需要样品的预处 理,检测速度快(秒级速度),不消耗试剂、绿色环保分析等特点,符合菌检快速检测的要 求,但是,能否利用近红外技术对细菌等微生物进行检测,检测结果的准确度如何?以往从 未见此方面的论文或报道。鉴于此,我们利用美国 Brimrose 公司的 Luminar 5030 型便携式 AOTF 技术近红外光谱仪对厦门中药厂有限公司提供的 20 个样品进行光谱采集,建立模型并 预测,以考察 AOTF-NIR 技术能否在菌检项目中成功应用。声光可调滤光器(Acousto-optic tunable filter,简称 AOTF)是基于各向异性的双折射晶体的声光衍射原理,利用超声波 与特定的晶体作用而产生分光的光电器件[2,3,4]。与传统的基于机械调谐分光元件的光谱仪器 相比,以 AOTF 作为分光元件的光谱仪具有明显的优越性:它结构简单,光学系统无移动性 部件,体积小,集光能力强,最吸引人之处在于它的扫描速度快、信噪比高[5]。
1. 实验部分
1.1 仪器条件和样品处理
仪器:美国 BRIMROSE 公司产的 Luminar 5030 型便携式 AOTF 技术近红外光谱仪,主要 部件包括:光学部分、控制部分、电源适配器、笔记本电脑。仪器波长范围为 1100nm 到 2300nm, 2nm 的波长增量,扫描次数为 300,采用 InGaAs 检测器。挪威 CAMO 公司 The Unscrambler 分析软件。
样品:新癀片不规则颗粒状样品 20 个,编号为 1-20,其中 1 号和 2 号样品中的微生物 已经杀死,为死菌体;3-20 号样品中的微生物为活菌体。并提供每个样品细菌数和霉菌数 的数据,单位为:个/克。见表 1 所示。
表 1: 样品的编号及微生物个数值
| 新癀片批号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 细菌数(个/g) | 10 | 10 | 10 | 10 | 10 | 10 | 500 | 10 | 10 | 10 |
| 霉菌数(个/g) | 50 | 10 | 1050 | 1400 | 1630 | 170 | 100 | 10 | 10 | 50 |
| 新癀片批号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 细菌数(个/g) | 300 | 1000 | 500 | 500 | 1000 | 1700 | 10 | 300 | 500 | 10 |
| 霉菌数(个/g) | 30 | 10 | 100 | 3550 | 600 | 250 | 4500 | 200 | 50 | 100 |
1.2 实验方法:
本次实验扫描新癀片样品数量 20 个,样品状态为不规则的颗粒状。使用美国 Brimrose 公司 Luminar 5030 型近红外光谱仪采集样品的光谱数据。将样品放置于样品盒的槽中,用 盒盖将样品刮平,连同盒盖一起放置于支架上,光谱仪的探头卡在样品盒盖的圆孔中,垂直 卡紧,采用漫反射的测样方式采集光谱。每一张光谱都是 300 次扫描的平均结果。波长范围 从 1100nm 到 2300nm,波长增量为 2nm。每个样品均连续扫描 5 张光谱,共得到 100 张光谱。 将 100 个光谱数据经过一阶微分处理(9 点平滑),导入 The Unscrambler 分析软件,然后 利用 PCA 对光谱数据进行计算创建定性校正模型;将细菌数和霉菌数的数据与样品一一对 应,采用 PLS1 方式进行计算建立定量校正模型。
1.3 光谱及预处理
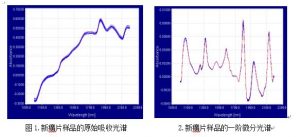
新癀片样品的原始吸收光谱(见图 5),从图中可以看出,所有光谱排列整齐有序,没 有异常的样品光谱。新癀片样品的一阶微分光谱(见图 6),同样整齐有序,有比较明显的 吸收峰,光谱排列更加紧密,光谱与光谱之间的相似性较强,采集到的光谱信息量大。
2.建立 PLS1 定量分析模型
2.1 模型的建立
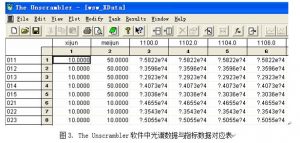
表 1 为所提供样品的编号及每个样品所对应的细菌数和霉菌数的数据。在 The Unscrambler 软件中,将每个样品的光谱数据与细菌和霉菌个数的数据一一对应,如图 3 所 示。
采用偏最小二乘法(PLS1),完全交互验证(Full Cross Validation)的方式建立细 菌和霉菌的回归定量分析模型。
2.2 结果分析
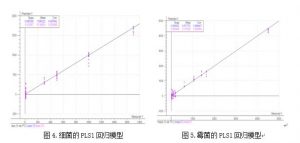
从图 4 图 5 的细菌和霉菌的回归模型看:两者都有很好的相关性,相关系数分别为 0.9791 和 0.9895。因此,我们可以初步判断利用近红外光谱可以得到微生物有效的信息。 因为建立模型所用的样品数量比较少,无法进行未知样品的验证,因此,我们用所建 立的模型对所有扫描的光谱进行一个内部的验证,所得到的结果与外部验证相似,可以说明
相同的问题。表 2 是调用模型对细菌和霉菌的一个验证结果:
表 2.模型对细菌和霉菌的预测结果
| 样品编号 | 细菌预测值 | 细菌实际值 | 霉菌预测值 | 霉菌实际值 |
| 11 | 23 | 10 | 510 | 50 |
| 12 | -42 | 10 | 33 | 50 |
| 13 | 105 | 10 | 66 | 50 |
| 14 | 17 | 10 | 205 | 50 |
| 15 | 44 | 10 | 373 | 50 |
| 21 | -121 | 10 | -192 | 10 |
| 22 | 8 | 10 | 59 | 10 |
| 23 | 32 | 10 | -13 | 10 |
| 24 | 34 | 10 | -85 | 10 |
| 25 | -187 | 10 | -82 | 10 |
| 31 | 38 | 10 | 1086 | 1050 |
| 32 | 214 | 10 | 1117 | 1050 |
| 33 | 13 | 10 | 1255 | 1050 |
| 34 | -39 | 10 | 993 | 1050 |
| 35 | 52 | 10 | 1152 | 1050 |
| 41 | 41 | 10 | 1666 | 1400 |
| 42 | -126 | 10 | 1593 | 1400 |
| 43 | -61 | 10 | 1407 | 1400 |
| 44 | -256 | 10 | 1409 | 1400 |
| 45 | -9 | 10 | 1409 | 1400 |
| 51 | 59 | 10 | 1483 | 1630 |
| 52 | 32 | 10 | 1645 | 1630 |
| 53 | 45 | 10 | 1429 | 1630 |
| 54 | -27 | 10 | 1652 | 1630 |
| 55 | -17 | 10 | 1378 | 1630 |
| 61 | 13 | 10 | 84 | 170 |
| 62 | -29 | 10 | 366 | 170 |
| 63 | 16 | 10 | 388 | 170 |
| 64 | 14 | 10 | 182 | 170 |
| 65 | 263 | 10 | 570 | 170 |
| 71 | 759 | 500 | 218 | 100 |
| 72 | 487 | 500 | -709 | 100 |
| 73 | 704 | 500 | -50 | 100 |
| 74 | 548 | 500 | 57 | 100 |
| 75 | 761 | 500 | -311 | 100 |
| 81 | 211 | 10 | 114 | 10 |
| 样品编号 | 细菌预测值 | 细菌实际值 | 霉菌预测值 | 霉菌实际值 |
| 82 | 38 | 10 | -97 | 10 |
| 83 | 80 | 10 | 377 | 10 |
| 84 | -44 | 10 | 394 | 10 |
| 85 | 18 | 10 | 78 | 10 |
| 91 | 3 | 10 | 648 | 10 |
| 92 | -9 | 10 | 108 | 10 |
| 93 | 129 | 10 | 646 | 10 |
| 94 | -216 | 10 | 479 | 10 |
| 95 | 28 | 10 | -56 | 10 |
| 101 | -9 | 10 | 527 | 50 |
| 102 | 80 | 10 | 340 | 50 |
| 103 | 1 | 10 | 102 | 50 |
| 104 | 5 | 10 | -32 | 50 |
| 105 | 9 | 10 | 70 | 50 |
| 111 | 235 | 300 | 77 | 30 |
| 112 | 257 | 300 | 52 | 30 |
| 113 | 240 | 300 | -136 | 30 |
| 114 | 299 | 300 | 59 | 30 |
| 115 | 286 | 300 | 129 | 30 |
| 121 | 986 | 1000 | 292 | 10 |
| 122 | 1147 | 1000 | 324 | 10 |
| 123 | 712 | 1000 | -47 | 10 |
| 124 | 975 | 1000 | 86 | 10 |
| 125 | 1032 | 1000 | 239 | 10 |
| 131 | 450 | 500 | 527 | 100 |
| 132 | 245 | 500 | 9 | 100 |
| 133 | 414 | 500 | 250 | 100 |
| 134 | 459 | 500 | 171 | 100 |
| 135 | 530 | 500 | 74 | 100 |
| 141 | 502 | 500 | 2525 | 3550 |
| 142 | 502 | 500 | ||
| 2776 | 3550 | |||
| 143 | 518 | 500 | ||
| 2125 | 3550 | |||
| 144 | ||||
| 454 | 500 | 2626 | 3550 | |
| 145 | 500 | 500 | ||
| 2427 | 3550 | |||
| 151 | 960 | 1000 | ||
| 721 | 600 | |||
| 152 | ||||
| 718 | 1000 | 690 | 600 | |
| 153 | 1036 | 1000 | ||
| 690 | 600 | |||
| 154 | 1001 | 1000 | ||
| 586 | 600 | |||
| 样品编号 | 细菌预测值 | 细菌实际值 | 霉菌预测值 | 霉菌实际值 |
| 155 | 1002 | 1000 | 615 | 600 |
| 161 | 1674 | 1700 | -334 | 250 |
| 162 | 1729 | 1700 | -163 | 250 |
| 163 | 1675 | 1700 | -284 | 250 |
| 164 | 1720 | 1700 | -226 | 250 |
| 165 | 1518 | 1700 | -381 | 250 |
| 171 | 85 | 10 | 4231 | 4500 |
| 172 | -9 | 10 | 4386 | 4500 |
| 173 | -6 | 10 | 4424 | 4500 |
| 174 | 34 | 10 | 4499 | 4500 |
| 175 | -36 | 10 | 4496 | 4500 |
| 181 | 284 | 300 | 211 | 200 |
| 182 | 283 | 300 | 7 | 200 |
| 183 | 292 | 300 | 201 | 200 |
| 184 | 280 | 300 | 170 | 200 |
| 185 | 183 | 300 | -147 | 200 |
| 191 | 471 | 500 | -157 | 50 |
| 192 | 653 | 500 | -355 | 50 |
| 193 | 499 | 500 | -70 | 50 |
| 194 | 496 | 500 | -461 | 50 |
| 195 | 521 | 500 | 70 | 50 |
| 201 | 79 | 10 | 886 | 100 |
| 202 | 298 | 10 | 984 | 100 |
| 203 | 221 | 10 | 873 | 100 |
| 204 | 63 | 10 | 714 | 100 |
| 205 | 237 | 10 | 662 | 100 |
从表 2 可以看出:细菌数量大于 300 个的样品和霉菌数量大于 600 个的样品的模型预 测结果都接近于实际值,比较准确。但是对数量比较少的样品预测的结果差别非常大。这是 因为两个模型的数据梯度非常大,数据从几个到几千,在这么宽的数据范围内,由于样品量 有限,没有很好的梯度间隔,而且,微生物个数少的样品其信号反应也相对较弱,因此,很 难预测其准确的个数。
2.3 模型的改进
针对细菌而言,如果我们的最终结果只是要求将细菌的个数控制一个数量之下,
比如少于 7000 个为合格,那么以上模型虽然对细菌少的样品预测不够准确,但能够达到控
制的要求。对于霉菌来说,国家标准要求是少于 100 个为合格,那么我们换一个思路,用霉
菌数量少于等于 100 个的样品建立霉菌的模型,看能够达到什么样的预测效果。在扫描的 100 个光谱中,霉菌数量 100 个以下的样品的光谱个数共为 55 个。利用这 55 个光谱数据和 对应的霉菌个数值,建立 100 个以下霉菌的模型,见图 6。
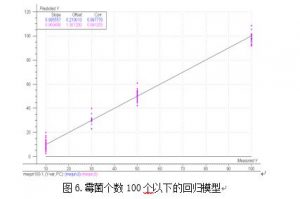
从图 6 可以看出,霉菌小范围模型有更好的相关性,相关系数达到了 0.9913,利用这个
模型对建模用的 55 个光谱进行预测,得到表 3 的结果。
表 3.霉菌 100 以下小范围模型预测结果与实际值的比较
| 样品 编号 | 预测值 | 实际值 | 绝对 偏差 | 样品 编号 | 预测值 | 实际值 | 绝对 偏差 |
| 11 | 50 | 50 | 0 | 104 | 53 | 50 | -3 |
| 12 | 46 | 50 | 4 | 105 | 51 | 50 | -1 |
| 13 | 54 | 50 | -4 | 111 | 32 | 30 | -2 |
| 14 | 48 | 50 | 2 | 112 | 27 | 30 | 3 |
| 15 | 51 | 50 | -1 | 113 | 31 | 30 | -1 |
| 21 | 12 | 10 | -2 | 114 | 36 | 30 | -6 |
| 22 | 11 | 10 | -1 | 115 | 30 | 30 | 0 |
| 23 | 9 | 10 | 1 | 121 | 9 | 10 | 1 |
| 24 | 10 | 10 | 0 | 122 | 11 | 10 | -1 |
| 25 | 7 | 10 | 3 | 123 | 11 | 10 | -1 |
| 71 | 98 | 100 | 2 | 124 | 11 | 10 | -1 |
| 72 | 100 | 100 | 0 | 125 | 7 | 10 | 3 |
| 73 | 101 | 100 | -1 | 131 | 100 | 100 | 0 |
| 74 | 97 | 100 | 3 | 132 | 101 | 100 | -1 |
| 75 | 100 | 100 | 0 | 133 | 96 | 100 | 4 |
| 81 | 11 | 10 | -1 | 134 | 98 | 100 | 2 |
| 82 | 14 | 10 | -4 | 135 | 97 | 100 | 3 |
| 样品 编号 | 预测值 | 实际值 | 绝对 偏差 | 样品 编号 | 预测值 | 实际值 | 绝对 偏差 |
| 83 | 9 | 10 | 1 | 191 | 51 | 50 | -1 |
| 84 | 6 | 10 | 4 | 192 | 53 | 50 | -3 |
| 85 | 12 | 10 | -2 | 193 | 50 | 50 | 0 |
| 91 | 8 | 10 | 2 | 194 | 53 | 50 | -3 |
| 92 | 8 | 10 | 2 | 195 | 51 | 50 | -1 |
| 93 | 10 | 10 | 0 | 201 | 99 | 100 | 1 |
| 94 | 8 | 10 | 2 | 202 | 100 | 100 | 0 |
| 95 | 7 | 10 | 3 | 203 | 105 | 100 | -5 |
| 101 | 53 | 50 | -3 | 204 | 98 | 100 | 2 |
| 102 | 48 | 50 | 2 | 205 | 97 | 100 | 3 |
| 103 | 54 | 50 | -4 |
从表 3 可以看出:霉菌的 100 以下小范围模型对 100 个以下的样品预测的结果准确度非 常高,只有正负几个的绝对偏差。小范围模型预测霉菌数量少的样品比较准确,那么预测霉 菌数量大于 100 个的样品的结果会怎么样?表 4 是霉菌数量大于 100 的样品的预测结果。
表 4.小范围模型预测霉菌数量大于 100 的样品的结果
| 样品编号 | 预测值 | 实际值 | 样品编号 | 预测值 | 实际值 |
| 31 | 103 | 1050 | 141 | 90 | 3550 |
| 32 | 112 | 1050 | 142 | 97 | 3550 |
| 33 | 105 | 1050 | 143 | 102 | 3550 |
| 34 | 103 | 1050 | 144 | 90 | 3550 |
| 35 | 107 | 1050 | 145 | 94 | 3550 |
| 41 | 149 | 1400 | 151 | 89 | 600 |
| 42 | 151 | 1400 | 152 | 93 | 600 |
| 43 | 158 | 1400 | 153 | 90 | 600 |
| 44 | 149 | 1400 | 154 | 94 | 600 |
| 45 | 142 | 1400 | 155 | 93 | 600 |
| 51 | 92 | 1630 | 161 | 89 | 250 |
| 52 | 85 | 1630 | 162 | 89 | 250 |
| 53 | 91 | 1630 | 163 | 91 | 250 |
| 54 | 84 | 1630 | 164 | 84 | 250 |
| 55 | 90 | 1630 | 165 | 90 | 250 |
| 61 | 21 | 170 | 171 | 106 | 4500 |
| 62 | 15 | 170 | 172 | 91 | 4500 |
| 63 | 12 | 170 | 173 | 108 | 4500 |
| 64 | 17 | 170 | 174 | 103 | 4500 |
| 样品编号 | 预测值 | 实际值 | 样品编号 | 预测值 | 实际值 |
| 65 | 13 | 170 | 175 | 101 | 4500 |
从表 4 可以看出:霉菌数量小于 100 的样品所建立的小范围测试模型预测霉菌数量大 于 100 的样品的结果与实际值相差很大,这是正常的,因为所测试的样品范围不在建模范围 之内,预测的结果肯定是不准确的。我们可以尝试用霉菌的数量小于 600 个的所有样品再建 立一个模型。在扫描的 100 个光谱中,霉菌数量小于 600 个的样品的光谱个数共为 75 个。 利用这 75 个光谱数据和对应的霉菌个数值,建立 600 个以下霉菌的模型,见图 7。
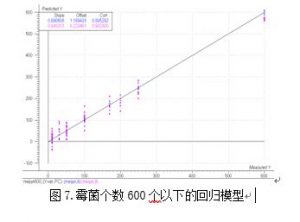
从图 7 可以看出,霉菌 600 个以下的模型也有很好的相关性,相关系数为 0.9823,利用
这个模型对建模用的 75 个光谱进行预测,得到表 5 的结果。
表 5.霉菌 600 个以下的模型预测霉菌数量小于 600 个的样品的结果
| 样品编号 | 预测值 | 实际值 | 样品编号 | 预测值 | 实际值 |
| 11 | 69 | 50 | 114 | 32 | 30 |
| 12 | 50 | 50 | 115 | 56 | 30 |
| 13 | 44 | 50 | 121 | -2 | 10 |
| 14 | 30 | 50 | 122 | 48 | 10 |
| 15 | 52 | 50 | 123 | -76 | 10 |
| 21 | 18 | 10 | 124 | 18 | 10 |
| 22 | -92 | 10 | 125 | -3 | 10 |
| 23 | 30 | 10 | 131 | 111 | 100 |
| 24 | 7 | 10 | 132 | 38 | 100 |
| 25 | -96 | 10 | 133 | 123 | 100 |
| 61 | 179 | 170 | 134 | 73 | 100 |
| 样品编号 | 预测值 | 实际值 | 样品编号 | 预测值 | 实际值 |
| 62 | 189 | 170 | 135 | 112 | 100 |
| 63 | 173 | 170 | 151 | 607 | 600 |
| 64 | 147 | 170 | 152 | 589 | 600 |
| 65 | 165 | 170 | 153 | 597 | 600 |
| 71 | 190 | 100 | 154 | 606 | 600 |
| 72 | 101 | 100 | 155 | 589 | 600 |
| 73 | 97 | 100 | 161 | 231 | 250 |
| 74 | 97 | 100 | 162 | 246 | 250 |
| 75 | 147 | 100 | 163 | 226 | 250 |
| 81 | 124 | 10 | 164 | 272 | 250 |
| 82 | 17 | 10 | 165 | 247 | 250 |
| 83 | 31 | 10 | 181 | 217 | 200 |
| 84 | 28 | 10 | 182 | 131 | 200 |
| 85 | -7 | 10 | 183 | 180 | 200 |
| 91 | 31 | 10 | 184 | 201 | 200 |
| 92 | 16 | 10 | 185 | 190 | 200 |
| 93 | 13 | 10 | 191 | 43 | 50 |
| 94 | -4 | 10 | 192 | 46 | 50 |
| 95 | -23 | 10 | 193 | 36 | 50 |
| 101 | 50 | 50 | 194 | 38 | 50 |
| 102 | 101 | 50 | 195 | -1 | 50 |
| 103 | 70 | 50 | 201 | 183 | 100 |
| 104 | 69 | 50 | 202 | 204 | 100 |
| 105 | 26 | 50 | 203 | 100 | 100 | |
| 111 | 15 | 30 | 204 | 95 | 100 | |
| 112 | 58 | 30 | 205 | 108 | 100 | |
| 113 | 10 | 30 |
从表 5 可以看出:霉菌 600 个以下的模型对霉菌数量为 170、200、250、600 个的四个 样品预测的结果准确度很高;对霉菌数量 100 个以下的样品预测准确度降低,但每个样品的 平均值仍然能够接近于实际值。
2.4 综合解决方案
综合以上的分析,在如此大的数据梯度范围内,我们没有办法只用一个模型就能够测 量准确所有的样品。但是,分析本次实验我们可以发现建立三个模型就可以准确预测每一个 样品的霉菌数量(细菌与此类似,不再作详细分析),这三个模型是:所有样品参与建立的 宽数据范围的综合模型,我们不妨称其为 model-all;霉菌数量小于 600 个样品建立的模型 称为 model-1000;霉菌数量小于 100 个样品建立的小范围模型称为 model-100。
分析表 2,霉菌个数在 1000 个以上的样品预测的非常准确,个数在 1000 个以下的样品 预测值没有超过 1000 的,因此,通过 model-all 的预测,可以有效地将霉菌个数在 1000 个 以上的样品进行准确检测。
分析表 5,利用 model-1000 模型,可以准确预测霉菌数量 100 个以上的样品。霉菌数 量 100 个以下的样品预测不够准确。
分析表 3,利用 model-100 模型,对霉菌数量在 100 个以下的样品预测的准确度非常高。
根据以上分析总结,完全可以利用 AOTF-NIR 技术,实现快速菌检的工作。步骤如下: 扫描未知样品的光谱,首先用 model-all 模型进行预测,预测值大于 1000,那么,该样品 的霉菌数量即为该数值;如果样品的预测值小于 1000,用 model-1000 模型再对该样品的光 谱进行预测,如果预测值在 200-1000 范围之内,那么我们可以肯定该样品的预测值为该样
品的真实值,如果预测值在 100-200 范围内,那么我们需要对该样品重复扫描 5 次,用 model-1000 模型预测 5 次光谱的平均值,即为该样品的真实值;如果用 model-1000 模型预 测该样品光谱的预测值小于 100,那么,再调用 model-100 模型对该样品进行准确的预测, 得到的结果就是该样品的实际值。
3.分析菌体数量是否合格
3.1 定性模型的建立
多模型分步快速菌检法非常适合 AOTF-NIR 技术在实验室快速对药品中的微生物进行检 测,但是,该方法相对复杂,不能够适应在线的快速微生物检测,下面我们来探讨一下用定 性分析的方法,能否解决在线菌检的工作。
还是以霉菌为例。定性分析和定量分析是两个不同的概念,定量分析可以检测到一个 样品中含有的霉菌的具体个数;定性分析是判断是与否的问题,假设规定药品中含有霉菌的 个数超过 100 个为不合格,少于 100 个为合格品,那么定性分析就是判断所检测的药品是否 合格的问题。
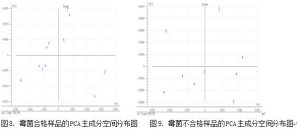
在已有的 20 个样品中,11 个样品的霉菌个数不超过 100,9 个样品的霉菌个数在 100 个以上。利用主成分分析(PCA)对 11 个样品的一阶微分光谱数据进行聚类,作为合格样品 集;对 9 个样品的一阶微分光谱数据进行聚类,作为不合格样品集。因为每个样品我们扫描 了 5 张光谱,我们可以将每个样品的第一张光谱分出来,作为验证用,其余的 4 个光谱参与 建立定性分析的模型。这样,合格样品集有 11 张验证光谱,不合格样品集有 9 张验证光谱。 44 张合格品光谱建立的定性模型为 yes,36 个不合格品样品建立的定性模型为 no,见图 8 和图 9。